Vektory
Vektor je geometrický objekt, ktorý je určený dĺžkou, smerom a orientáciou. Môžeme si ho predstaviť ako orientovanú úsečku, t. j. úsečku, na ktorej je vyznačený začiatočný a koncový bod. Pritom nesmieme zabudnúť, že dve rôzne orientované úsečky, ktoré majú zhodnú dĺžku (t. j. veľkosť), smer aj orientáciu, predstavujú ten istý vektor, ide o dve rôzne umiestnenia toho istého vektora.
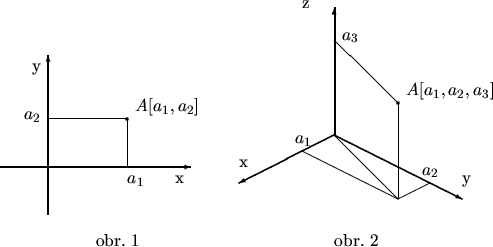
Súradnice vektora sú súradnice jeho koncového bodu v takom umiestnení vektora, keď začiatočný bod je zhodný so začiatkom súradnicovej sústavy. Fakt, že vektor ![]() má súradnice
má súradnice ![]() budeme zapisovať
budeme zapisovať ![]() . Teda, ak
. Teda, ak ![]() a
a ![]() , tak vektor so začiatočným bodom
, tak vektor so začiatočným bodom ![]() a koncovým bodom
a koncovým bodom ![]() má súradnice
má súradnice ![]() . Preto takýto vektor budeme označovať symbolom
. Preto takýto vektor budeme označovať symbolom ![]() .
.
Polohovým vektorom bodu ![]() rozumieme vektor
rozumieme vektor ![]() .
.
Dĺžka vektora ![]() je vzdialenosť jeho začiatočného a koncového bodu a označujeme ju
je vzdialenosť jeho začiatočného a koncového bodu a označujeme ju ![]() . Platí
. Platí
Jednotkový vektor je každý vektor, ktorého dĺžka je rovná
V ďalšom texte predpokladajme, že
Skalárny násobok vektora
- dĺžka vektora
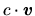 je
je 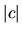 násobkom dĺžky vektora
násobkom dĺžky vektora 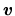
- obidva vektory majú rovnaký smer
-
- ak
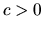 , tak
, tak 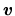 a
a 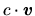 majú zhodnú orientáciu
majú zhodnú orientáciu - ak
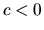 , tak
, tak 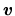 a
a 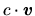 majú opačnú orientáciu
majú opačnú orientáciu - ak
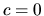 , tak
, tak 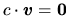 .
.
- ak
Vektor
Platí: Dva nenulové vektory sú rovnobežné práve vtedy, ak jeden z nich je skalárnym násobkom druhého. Je to práve vtedy, ak podiely ich prvých, druhých aj tretích súradníc sú zhodné.
Smerový vektor priamky ![]() je každý vektor rovnobežný s priamkou
je každý vektor rovnobežný s priamkou ![]() .
.
Normálový vektor priamky ![]() je každý vektor kolmý na priamku
je každý vektor kolmý na priamku ![]() .
.
Smerový vektor roviny ![]() je každý vektor rovnobežný s rovinou
je každý vektor rovnobežný s rovinou ![]() .
.
Normálový vektor roviny ![]() je každý vektor kolmý na rovinu
je každý vektor kolmý na rovinu ![]() .
.
Poznamenajme, že ak niektorý vektor je smerovým alebo normálovým vektorom priamky alebo roviny, tak aj jeho ľubovoľný nenulový skalárny násobok je taký. To znamená, že každá priamka alebo rovina má nekonečne veľa smerových a normálových vektorov. Dôležité však je, že
- ak máme určenú priamku v rovine, tak smery jej normálového a smerového vektora sú jednoznačne určené
- ak máme určenú priamku v priestore, tak smer jej smerového vektora je jednoznačne určený, avšak má nekonečne veľa normálových vektorov rôznych smerov
- ak máme určenú rovinu v priestore, tak smer jej normálového vektora je jednoznačne určený, avšak má nekonečne veľa smerových vektorov rôznych smerov.
Zdroj : https://www.youtube.com/watch?v=yizjn_juTRc
Toto použité video sme nevytvorili.
